Un’equazione si dice goniometrica se in essa compare qualche funzione goniometrica nel cui argomento figura l’incognita.

Per esempio:                                 

3 cos x = 2;        sen ² x – tg x = 1

sono funzioni goniometriche, mentre:

2 sen π – x = 3

non è un’equazione goniometrica bensì algebrica in x, dato che sen π è un numero e non una funzione goniometrica.

Equazioni elementari

Le equazioni goniometriche elementari sono del tipo:

sen x > b, cos x - b < 0,    tg x ≤  b, …

con  -1 ≤  b ≤  1 per le equazioni in seno e coseno, essendo funzioni limitate tra questi due valori;  mentre per ogni valore di b  per l’equazione in tangente, che è una funzione illimitata.

Ci sono due metodi per la loro risoluzione quello grafico e quello della circonferenza goniometrica. Noi utilizzeremo per la loro risoluzione il Metodo della Circonferenza goniometrica e la definizione delle funzioni goniometriche.

EQUAZIONI  ELEMENTARI IN SENO

Scriviamo l’equazione nella forma canonica:

si tratta di determinare quegli angoli x aventi un dato seno b.

Poiché il seno di un angolo rappresenta l’ordinata del punto della circonferenza goniometrica, risolvere l’equazione data significa determinare gli angoli associati ovvero corrispondenti ai punti della circonferenza goniometrica aventi stessa ordinata b.

Il problema pertanto si risolve trovando questi punti della circonferenza goniometrica, in quanto una volta trovati questi si individuano i corrispondenti angoli al centro che sono le soluzioni quindi dell’equazione data.

Vediamo dunque in generale i vari passi risolutori:

1. consideriamo dapprima l’equazione

ovvero determiniamo gli angoli x che si individuano in una sola circonferenza, ovvero in un angolo giro.     

Per quanto detto, dobbiamo determinare i  punti della circonferenza  goniometrica aventi stessa ordinata b e di conseguenza le soluzioni sono le ampiezze degli angoli ad essi associati

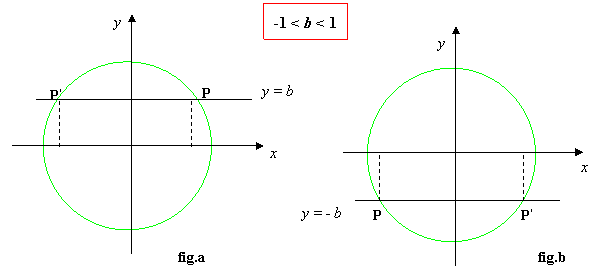
2. determiniamo tali punti: disegniamo nel piano cartesiano la circonferenza goniometrica e la retta parallela all’asse delle x:  y = b che come sappiamo è il luogo dei punti del piano aventi medesima ordinata; tale retta, se -1< b <1,  intersecherà la circonferenza in due punti distinti P e P’, aventi evidentemente stessa ordinata b che, per definizione, rappresenta il seno: e precisamente

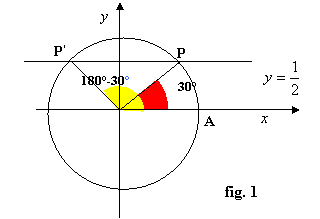
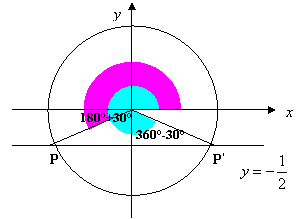
3. Determiniamo gli angoli associati ai punti: a tal scopo, congiungiamo i due punti P e P’ al centro della circonferenza e consideriamo i due angoli associati aventi come lato origine OA, essendo A(0,1) origine di tutti gli archi, e aventi come secondo lato rispettivamente OP e OP’; indichiamo con a il minimo angolo, cioè quello che cade nel primo quadrante, tale che sen a = I b I; vedi figure:

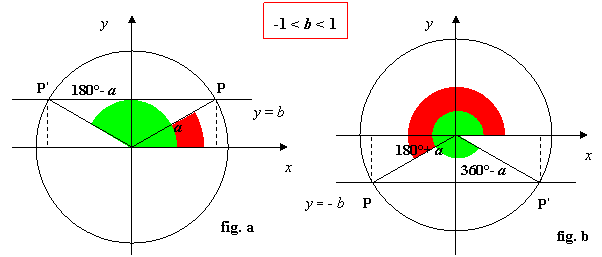
4. Le soluzioni: come si osserva in figura, i due angoli associati, soluzioni dell’equazione, sono supplementari (che come ricorderai dagli angoli associati, hanno uguale seno!): a e 180° - a ( fig.a) oppure 180° + a e 360° - a (fig.b) a seconda del segno di b . In generale, per la determinazione delle soluzioni in gradi o in radiante, si ha il seguente schema:

Schema Riepilogativo

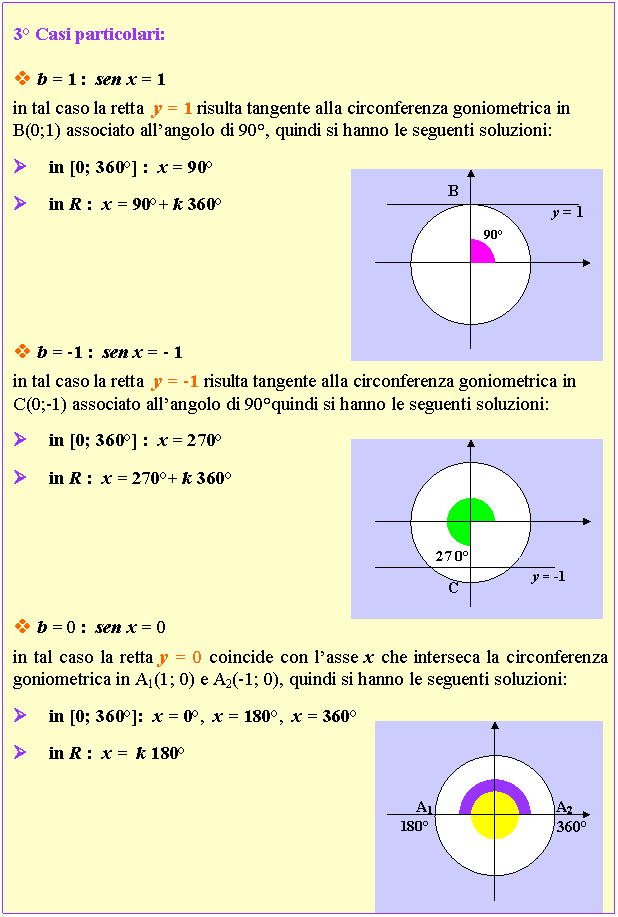
ESERCIZI SVOLTI

Risolvere le seguenti equazioni goniometriche elementari in seno:

Da quanto detto oppure ricordando che angoli supplementari hanno lo  stesso seno, possiamo dunque dire che limitandoci all’intervallo [0°; 360°]:

affinché due angoli abbiano lo stesso seno è necessario e sufficiente che abbiano uguali gli angoli oppure che uno di essi differisce dal supplementare dell’altro ( a meno dei multipli di 360°):

(*)   sen α = sen β ↔ α = β V α = 180° - β

Quindi se dobbiamo risolvere l’equazione seguente: