Un’equazione di primo grado in seno e coseno del tipo

con a, b, c numeri  reali e diversi da zero si dice equazione lineare in seno e coseno.

Se c = 0  ma a, b ≠ 0  l’equazione diventa

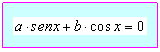
che è un’equazione lineare omogenea in seno e coseno.

v Risoluzione dell’equazione lineare omogenea in seno e coseno :

Dividiamo singolarmente i termine di ambo i membri per cosx, cosa lecita dato che è cosx ≠ 0,  ovvero x ≠ 90° + k360°, (infatti se fosse cos x = 0, sarebbe sen x = ± 1, perché quando il coseno assume il valore zero a 90° , 270°,….ecc. ,il seno vale 1 o -1, e l’equazione si ridurrebbe alla forma  ± a = 0 quando invece è per ipotesi a ≠ 0 ), ottenendo l’equazione elementare in  tg x:

      che sappiamo come risolvere.

Esercizio Svolto

Risolvere la seguente equazione:

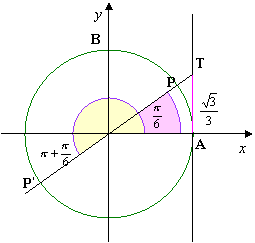
come si osserva le soluzioni sono:

v Risoluzione dell’equazione lineare non omogenea in seno e coseno

(1)   a sen x + b cos x + c = 0

Ø METODO ALGEBRICO

Esprimiamo sen x  e  cos x in funzione di , mediante le formule parametriche:

ottenendo:

che, in generale, è un’equazione di 2° grado in  t che risolta dà le soluzioni  t₁  e  t₂ da cui poi si risalirà alle soluzioni x₁ e x₂ dell’equazione lineare (1) mediante la posizione (*). Però, avendo introdotto l’incognita , l’equazione (2) non è del tutto   equivalente alla (1), in quanto abbiamo scartato i valori x = 180° + k360° che potrebbero invece essere soluzioni della (1); quindi si dovrà verificare se la (1) ammette per soluzioni anche x ≠ 180° + k360°. In tal caso queste verranno aggiunte alle soluzioni ottenute dalla (2).

Esercizio Svolto

Risolvere la seguente equazione lineare in seno e coseno con metodo algebrico:

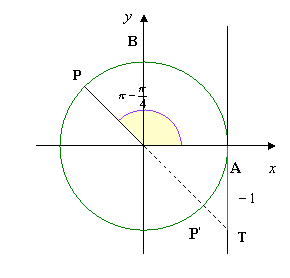
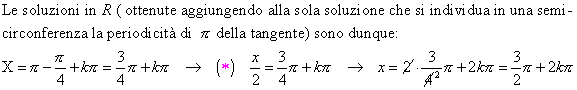
Dobbiamo infine verificare se i valori x = π + 2kπ  escluse dalla (●) sono soluzioni dell’equazione data; a tal scopo sarà sufficiente, per la periodicità,  sostituire alla x il solo valore π:

sen π – cos π + 1 = 0  →   0 - (- 1) + 1 = 0  →  2 ≠ 0

non essendo verificata l’uguaglianza,  x = π + 2 kπ  non sono soluzioni dell’equazione.

Ø METODO GRAFICO

Associamo all’equazione lineare non omogenea:

(1)   a sen x + b cos x + c = 0

la prima relazione fondamentale:

sen ² x + cos ² x = 1

ottenendo il sistema equivalente all’equazione data:

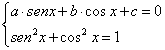
Poniamo poi  cos x = X   e  sen x = Y  ottenendo il seguente sistema algebrico:

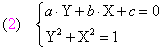
che risolto, con il metodo di sostituzione, troviamo le soluzioni X e Y , ovvero i valori di  cos x e  sen x, ottenendo dunque equazioni elementari da cui si risale ai valori degli angoli  x  soluzioni dell’equazione data (1) .

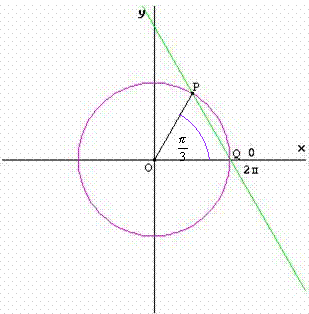
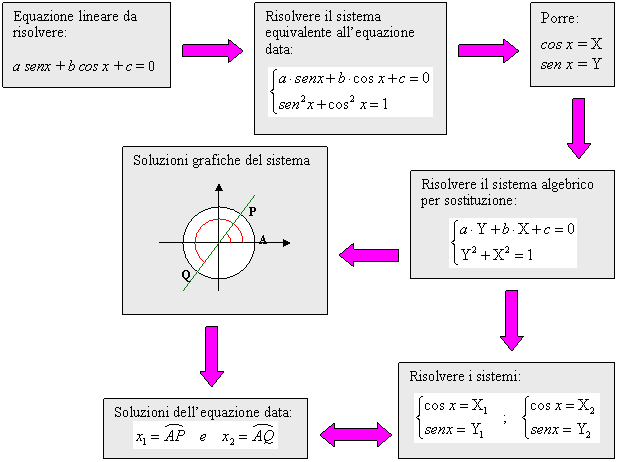
Tale metodo è detto grafico perché, dal punto di vista della geometria analitica, il sistema (2) non significa altro che determinare nel piano cartesiano i punti di intersezione della retta   aX + bY + c = 0   con la circonferenza  X² + Y² = 1, di centro l’origine e raggio 1, che coincide con la circonferenza goniometrica. Le eventuali soluzioni del sistema sono quindi  i punti della circonferenza goniometrica associati agli angoli-soluzioni dell’equazione data (1).

Schematizzazione del metodo grafico

Esercizio svolto

Risolvere la seguente equazione lineare non omogenea in seno e coseno con metodo grafico:

Le soluzioni trovate non sono altro che gli angoli associati ai punti P e Q d’intersezione della retta con la circonferenza goniometrica rappresentate graficamente nel piano cartesiano, vedi figura: