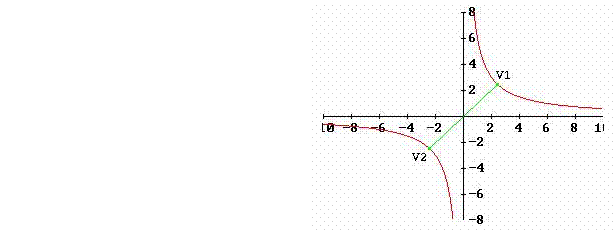
L’Iperbole è il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi detti fuochi
Supponiamo di prendere i due fuochi sull’asse x in posizione simmetrica rispetto all’asse y (che dunque passa per il punto medio del segmento che li congiunge), ossia F1(-c, 0) e F2(c, 0) e sia P(x, y) un punto qualsiasi dell’iperbole, in base alla definizione si ha che:
( 1 ) P F1 - P F2 = 2a con P F1 > P F2
avendo indicato con a una costante e con P F1 e P F2 le distanze del punto generico P dai fuochi.
Sotto queste condizioni, ovvero con i fuochi situati sull’asse x e disposti simmetricamente rispetto all’origine, nel piano cartesiano l’ellisse (in forma canonica) si presenta così:
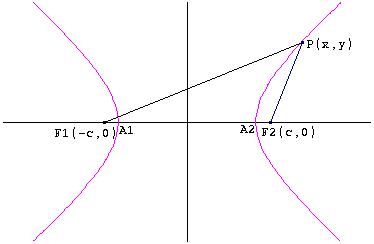
Con A1A2 = 2a, quindi A1(-a,0) e A2(a,0).
Utilizzando la definizione data dell’ellisse si perviene al suo modello algebrico: infatti per determinarla, basta imporre che un generico punto P(x,y) del piano soddisfi la proprietà caratteristica (1) e quindi calcolate le distanze PF1 e PF2 ed applicate le procedure risolutive per eliminare i radicali presenti (mediante isolamenti a primo membro di un radicale e successivi elevamenti al quadrato di ambo membri dell’equazione), si pone a 2- c 2 = b 2 per semplificare l’equazione pervenendo alla seguente:
Equazione canonica dell’iperbole
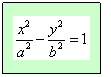
Caratteristiche:
v l’iperbole è simmetrica rispetto agli assi, detti assi di simmetria, e rispetto all’origine, detto centro di simmetria: quindi se P(x, y) è un suo punto anche P1(-x, y), P2(x, -y), P3(-x, -y) saranno punti dell’iperbole
v A1(-a, 0) e A2(a, 0), punti d’intersezioni con l’asse x, sono detti vertici reali dell’iperbole e la retta che passa per essi prende il nome di asse reale o asse trasverso o asse focale, perché vi si trovano i due fuochi; mentre non si hanno intersezioni reali con l’asse y e di conseguenza B1(-b, 0) e B2(b, 0) sono detti vertici immaginari e la retta passante per essi prende il nome di asse immaginario; OA1 = OA2 = a prende il nome di semiasse reale mentre OB1 = OB2 = b semiasse immaginario; OF1 = F2 = 2c prende il nome di semidistanza focale
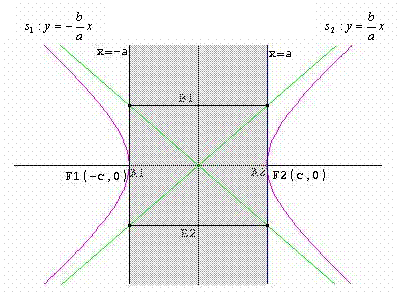
v come si osserva in figura, l’iperbole è tutta situatala di fuori della striscia di piano compresa tra le rette x = -a e x = a ed è illimitata sia nella direzione dell’asse x che nella direzione dell’asse y, in entrambi i sensi
v l’iperbole è tutta contenuta all’interno degli angoli formate dalle due rette s1 e s2 di equazioni:
individuate dalle diagonali del rettangolo associato ai vertici reali A1A2 e ai vertici immaginari B1B2 dell’iperbole e dette asintoti dell’iperbole, i cui rami si avvicinano indefinitamente senza mai incontrarle
v si definisce eccentricità:
perché per ogni iperbole si ha sempre che c > a: lo schiacciamento dell’iperbole sul suo asse reale è tanto più evidente quanto più la sua eccentricità è prossima a 1
Osservazione:
Per rappresentare graficamente l’iperbole, è conveniente tracciare dapprima gli asintoti, calcolare le coordinate dei vertici e poi, eventualmente ricavando altri punti, disegnare la curva.
Ø Iperbole Equilatera riferita agli assi
Se le
lunghezze degli assi 
, ovvero se i coefficienti numerici dell’equazione
sono uguali fra loro (a = b) si ottiene l’equazione:
cioè si riduce alla forma:
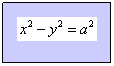
e si ha l’iperbole equilatera riferita agli assi, così chiamata perché gli assi di simmetria sono gli assi cartesiani.
Questa iperbole presenta le seguenti particolarità:
v i vertici si trovano nei punti (-a,0) e (a,0)
v gli asintoti dell’iperbole equilatera hanno equazioni:
ossia sono le bisettrici dei quadranti
v le coordinate dei fuochi sono:
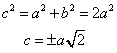
v l’eccentricità
Il suo grafico è il seguente:
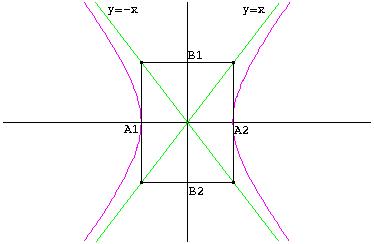
Ø Iperbole Equilatera riferita agli asintoti
Considerata l’iperbole equilatera riferita ai suoi assi, ruotando gli assi cartesiani di 45°, essi vengono a trovarsi coincidenti con gli asintoti dell’iperbole, si ha quindi l’iperbole equilatera riferita agli asintoti, in cui gli asintoti sono gli assi cartesiani.
Con la rotazione degli assi cambia l’equazione dell’iperbole equilatera (sfruttando conoscenze sul seno ed il coseno degli angoli) ed assume la forma:
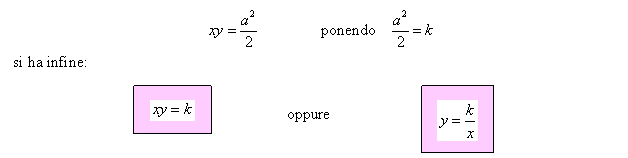
Si hanno i seguenti due casi di grafici:
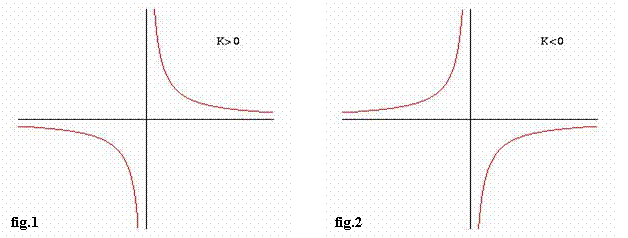
Quindi:
v
se k > 0, ovvero se le coordinate sono concordi,
allora i due rami di iperbole si trovano nel primo e terzo quadrante e i vertici
hanno coordinate 
, vedi fig.1
v
se k < 0,ovvero le coordinate sono discordi,
allora i due rami di iperbole si trovano nel secondo e quarto quadrante e i vertici
hanno coordinate 
, vedi fig.2
v gli asintoti sono le rette x = 0 e y = 0, ossia gli assi cartesiani
L’iperbole equilatera riferita agli asintoti esprime la proporzionalità inversa tra le grandezze.
Osservazioni: Per determinare l’equazione canonica dell’iperbole, poiché in essa sono presenti (come nell’ellisse) due parametri incogniti a e b, è sufficiente che vengano assegnate solo due condizioni; mentre per determinare l'equazione dell’iperbole equilatera, riferita ai suoi assi oppure ai suoi asintoti, dato che vi è un solo parametro da calcolare ( a oppure k) è sufficiente che sia assegnata una sola condizione.
Problemi Svolti
1. Problema
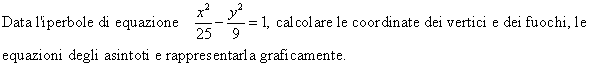
Risoluzione
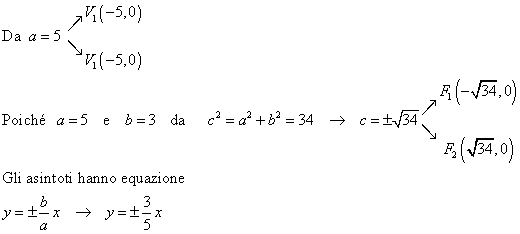
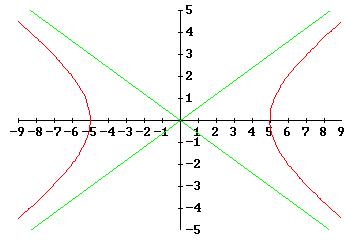
Per rappresentare l’iperbole tracciamo dapprima gli asintoti, le coordinate dei vertici e poi, disegniamo approssimativamente i due rami simmetrici della curva all’interno degli angoli formate dai due asintoti, senza necessariamente ricavare altri punti.
2. Problema
Determinare
l’equazione canonica dell’iperbole, con i fuochi appartenenti all’asse x,
passante per i punti A(5,6) e B
e rappresentarla graficamente.
Risoluzione
L’equazione canonica è del tipo:
Poiché la curva passa per A e B, le coordinate dei punti devono soddisfare l’equazione quindi si ha il seguente sistema:
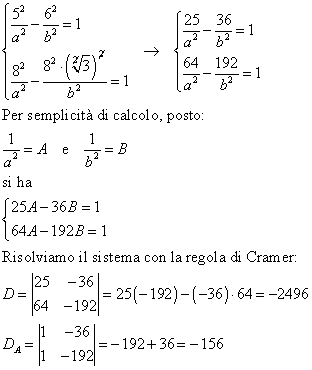
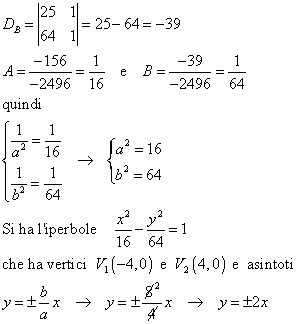
Rappresentiamo la curva:
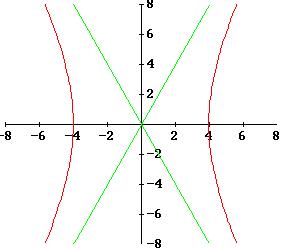
3. Problema
Determinare le equazioni dell’iperbole equilatera riferita agli assi e agli asintoti passanti per A(3,2) e rappresentarne i relativi grafici.
Risoluzione
Imponiamo alle iperbole il passaggio per A, ottenendo:
§
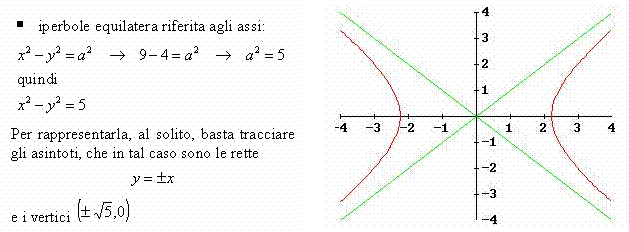
Iperbole equilatera riferita agli asintoti: x y = k → 3. 2 = k → k = 6 quindi xy = 6 Gli asintoti
sono gli assi cartesiani. Essendo k >0, i rami della curva si
trovano nel 1° e 3° quadrante, pertanto i vertici sono:
