La parabola è il luogo geometrico dei punti del piano equidistanti da un punto fisso F, detto fuoco, e da una retta fissa d, detta direttrice:

Partendo dalla caratteristica dei suoi punti, la parabola con asse di simmetria parallelo all’asse delle y ha equazione generale del tipo( funzione  quadratica):

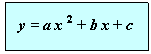
con a, b, c coefficienti reali e  a ≠ 0  ( altrimenti si ha una retta)

La concavità e l’apertura della parabola dipendono dal solo coefficiente a:

§ se a > 0  la parabola volge la concavità verso l’alto e quindi il vertice è il punto di minima                      ordinata, fig.1

§ se a < 0  la parabola volge la concavità verso il basso e quindi il vertice è il punto di massima ordinata, fig.2

§ all’aumentare di I a I (valore assoluto di a) diminuisce l’apertura della parabola, ossia la parabola si stringe al proprio asse di simmetria, fig.3 e fig.4

y = x ² – 2 x – 3