Prima di trattare le disequazioni goniometriche, è bene ricordare che:

Una disequazione si dice goniometrica se che contiene qualche funzione goniometrica nel cui argomento figura l’incognita .

Per le disequazioni goniometriche valgono gli stessi principi delle disequazioni algebriche; però bisogna tener presente il dominio, il codominio e la periodicità delle singole funzioni goniometriche: è bene rivedere la lezione Premesse ai modelli goniometrici prima di affrontare le disequazioni goniometriche.

Dapprima affronteremo lo studio di disequazioni elementari e successivamente prenderemo in esame alcune non elementari però ad esse riconducibili.

Disequazioni elementari sono del tipo:

sen x > b, cos x - b < 0, tg x ≤ b, …

con -1 ≤ b ≤ 1 per le disequazioni in seno e coseno, essendo funzioni limitate tra questi due valori ; mentre per ogni valore di b per la disequazione in tangente, che è una funzione illimitata.

Ci sono due metodi per la loro risoluzione quello grafico e quello della circonferenza goniometrica. Noi utilizzeremo per la loro risoluzione il Metodo della Circonferenza e la definizione delle funzioni goniometriche.

1. DISEQUAZIONI ELEMENTARI IN SENO

Scriviamo la disequazione in forma canonica:

sen x > b o sen x < b con -1 ≤ b ≤ 1

dove al posto di “ < “ o “ > “ può esserci il simbolo di “ ≤ ” o “≥” .

Si tratta di determinare per quali valori dell’angolo x il seno assume valori maggiori oppure minori di b.

Poiché il seno di un angolo rappresenta l’ordinata del punto della circonferenza goniometrica, risolvere le disequazioni date significa determinare gli angoli associati o corrispondenti ai punti della circonferenza goniometrica aventi ordinata maggiore oppure minore di b.

Il problema pertanto si risolve trovando questi punti e, quindi, gli angoli al centro ad essi associati.

In generale:

1. consideriamo l’equazione ad essa associata:

Dobbiamo pertanto determinare i punti della circonferenza goniometrica aventi ordinata b e

di conseguenza le soluzioni sono le ampiezze degli angoli ad essi associati

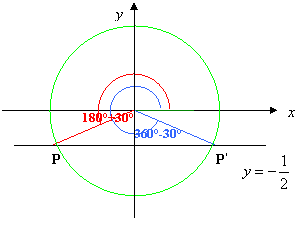
2. Determiniamo tali punti: disegniamo la circonferenza goniometrica e la retta parallela all’asse delle x, y = b; tale retta, se -1≤ b ≤1, intersecherà la circonferenza in due punti P e P’, aventi stessa ordinata b, vedi figure:

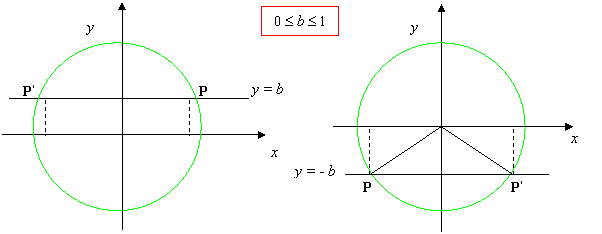
3. Determiniamo gli angoli associati ai punti: congiungiamo i punti P e P’ al centro della circonferenza e consideriamo i due angoli associati aventi come lato origine OA, essendo A(0,1)

origine di tutti gli archi, e aventi come secondo lato rispettivamente OP e OP’; indichiamo con a il minimo angolo, cioè che cade nel primo quadrante, tale che sen a = I b I, vedi figure:

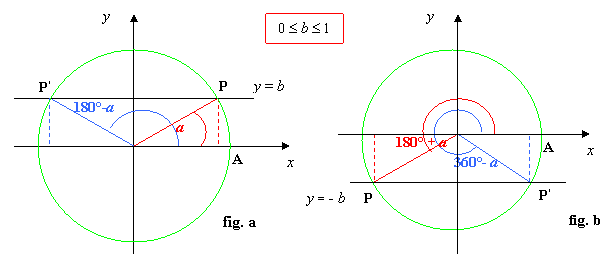
4. Per determinare le soluzioni si osserva il verso della disequazione data :

§ se è strettamente “ > “ o “ < “ i punti associati agli angoli vengono esclusi; in caso di “ ≤ ” o “≥” tali punti saranno inclusi tra le soluzioni della disequazione

§ se è sen x > b allora le soluzioni sono date dai punti della parte di circonferenza o dell’arco, che sta al di sopra della retta y = b; precisamente partendo sempre dall’origine A degli archi si ha:

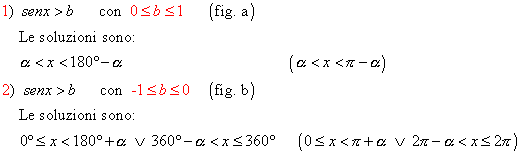
§ se è sen x < b allora le soluzioni sono date dai punti della parte di circonferenza o dell’arco, che sta al di sotto della retta y = b; precisamente:

5. Per determinare tutte le infinite soluzioni in R: aggiungiamo alle soluzioni trovate in [0;360°] i multipli di 360° ( 2 π ), per la periodicità della funzione seno, ovvero k360° (2kπ).

ESERCIZI GUIDATI

Risolvere le seguenti disequazioni goniometriche elementari in seno:

2. DISEQUAZIONI ELEMENTARI IN COSENO

Scriviamo la disequazione in forma canonica:

cos x > b o cos x < b con -1 ≤ b ≤ 1

dove al posto di “ < “ o “ > “ può esserci il simbolo di “ ≤ ” o “≥” .

Si tratta di determinare per quali valori dell’angolo x il coseno assume valori maggiori oppure minori di b.

Poiché il coseno di un angolo rappresenta l’ascissa del punto della circonferenza goniometrica, risolvere le disequazioni date significa determinare gli angoli corrispondenti ai punti della circonferenza goniometrica aventi ascissa maggiore oppure minore di b.

Il problema pertanto si risolve ancora trovando questi punti e, quindi, gli angoli al centro ad essi associati.

In generale:

1. consideriamo l’equazione ad essa associata:

Si tratta di determinare i punti della circonferenza goniometrica aventi ascissa b e di conseguenza le soluzioni sono le ampiezze degli angoli ad essi associati.

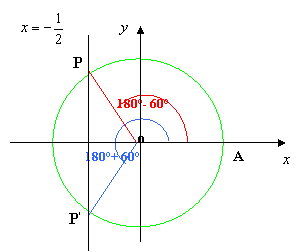
2. Determiniamo tali punti : disegniamo la circonferenza goniometrica e la retta parallela all’asse delle y, x = b; tale retta, se -1≤ b ≤1, intersecherà la circonferenza in due punti P e P’, aventi stessa ascissa b, vedi figure:

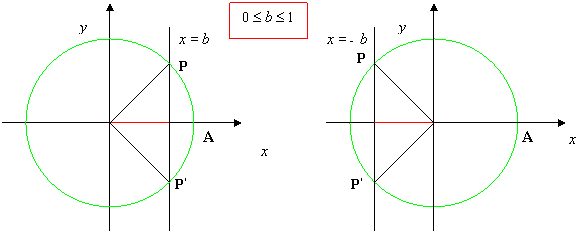
3. Determiniamo gli angoli associati ai punti: congiungiamo i punti P e P’ al centro della circonferenza e consideriamo i due angoli associati aventi come lato origine OA e aventi come secondo lato rispettivamente OP e OP’; indichiamo con a il minimo angolo tale che cos x = I b I, vedi figure:

4. Per determinare le soluzioni si osserva il verso della disequazione data :

§ se è strettamente “ > “ o “ < “ i punti associati agli angoli vengono esclusi; in caso di “ ≤ ” o “≥” tali punti saranno inclusi tra le soluzioni della disequazione

§ se è cos x > b allora le soluzioni sono date dai punti della parte di circonferenza o dell’arco, che sta a destra della retta x = b; precisamente, partendo dall’origine A degli archi si ha:

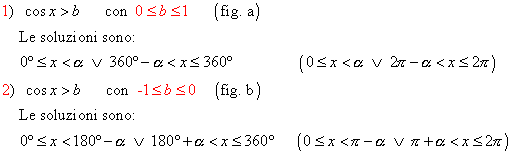
§ se è cos x < b allora le soluzioni sono date dai punti della parte di circonferenza o dell’arco, che sta a sinistra della retta x = b; precisamente:

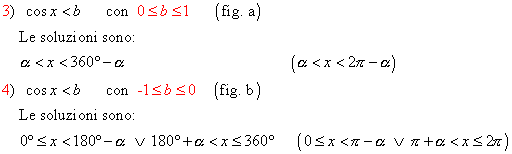
5. Per determinare le infinite soluzioni in R: aggiungiamo alle soluzioni trovate in [0; 360°] i multipli di 360° ( 2 π ), per la periodicità della funzione seno.

ESERCIZI GUIDATI

Risolvere le seguenti disequazioni goniometriche elementari in coseno:

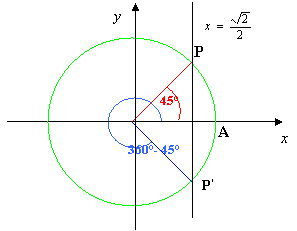
Le soluzioni dell’equazione associata sono dunque: x = 120° e x = 240°

Mentre le soluzioni della disequazione sono dati dagli angoli associati ai punti dell’arco di circonferenza situato a sinistra della retta , esclusi i punti, ovvero:

120° < x < 240°

3. DISEQUAZIONI ELEMENTARI IN TANGENTE

Scriviamo la disequazione in forma canonica:

tg x > b o tg x < b con - ∞ < b < + ∞

dove al posto di “ < “ o “ > “ può esserci il simbolo di “ ≤ ” o “≥” .

Si tratta di determinare per quali valori dell’angolo x la tangente assume valori maggiori oppure minori di b.

In generale:

1. consideriamo l’equazione ad essa associata:

Si tratta di determinare i punti della circonferenza goniometrica aventi stessa tangente e di conseguenza le soluzioni sono le ampiezze degli angoli ad essi associati.

2. Determiniamo tali punti : disegniamo la circonferenza goniometrica e la retta tangente alla circonferenza nel punto A, origine degli archi. Su tale retta individuiamo il punto T la cui ordinata è b. Tracciamo la retta del diametro passante per T; questa incontra la circonferenza nei due punti P e P’ aventi la tangente uguale a b, vedi figure:

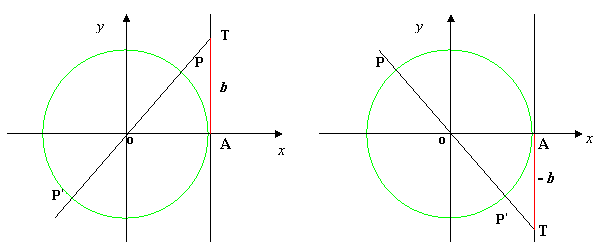
3. Determiniamo gli angoli associati ai punti: partendo, al solito, dall’ origine A degli archi si individuano i due angoli AÔP e AÔP’ angoli associati ai punti P e P’aventi stessa tangente; con a il minimo angolo tale che tg x = I b I, cioè a è l’ampiezza dell’angolo positivo,vedi figure:

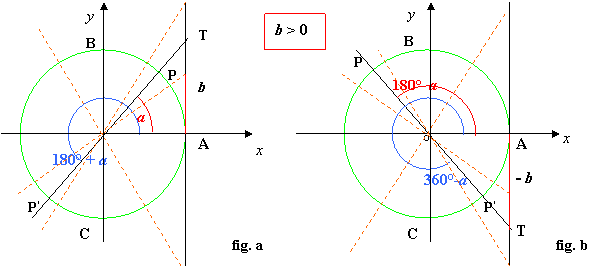
4. Per determinare le soluzioni si osserva il verso della disequazione data :

§ se è strettamente “ > “ o “ < “ i punti associati agli angoli vengono esclusi; in caso di “ ≤ ” o “≥” tali punti saranno inclusi tra le soluzioni della disequazione

§ se è tg x > b , come in fig. a, osservando le rette del diametro tratteggiate e passanti per T, si intuisce che le soluzioni sono date dagli angoli associati ai punti che stanno o nell’arco PB o nell’arco P’C, esclusi oltre i punti B e C, perché a 90° e a 270° non è definita la tangente , anche i punti P e P’ perché la disuguaglianza è stretta; mentre osservando la fig. b le soluzioni sono date dagli angoli associati ai punti che stanno sugli archi AB , PC e P’A, esclusi oltre i punti B e C anche i punti P e P’; precisamente:

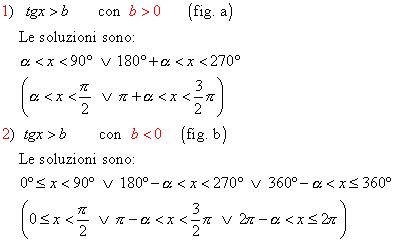
§ se è tg x < b , come in fig. a, osservando le rette del diametro tratteggiate e passanti per T, si intuisce che le soluzioni sono date dagli angoli associati ai punti che stanno sugli archi AP, BP’ e CA, esclusi oltre i punti B e C, ove non esiste la tangente, anche i punti P e P’ perché la disuguaglianza è stretta; mentre osservando la fig. b le soluzioni sono date dagli angoli associati ai punti che stanno sugli archi BP e CP’, esclusi i punti; precisamente:

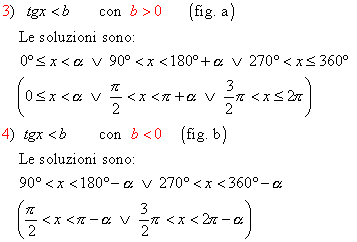
5. Per determinare le infinite soluzioni in R: si aggiungono alle soluzioni che cadono solo in [0°;180°] i multipli di 180° ( π ), per la periodicità della funzione tangente: x = a + k180° oppure x = a + kπ .

ESERCIZI GUIDATI

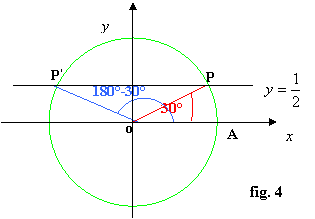
Risolvere le seguenti disequazioni goniometriche elementari in tangente:

1) tgx < 1 con 0° ≤ x ≤ 360°

Con l’aiuto della circonferenza goniometrica e la definizione di tangente di un angolo, ricerchiamo gli angoli x la cui tangente è 1.

Disegniamo, dunque, la circonferenza goniometrica e la retta ad essa tangente nel punto A; riportiamo sulla retta il punto T di ordinata 1. Tracciamo la retta del diametro passante per T che intersecherà la circonferenza nei due punti P e P’ ai quali corrispondono gli angoli a e 180° + a, con a = 45° essendo tg 45° =1, vedi figura :

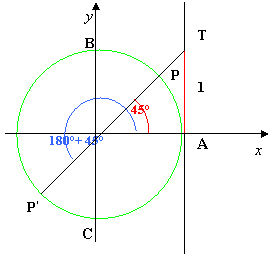
Quindi le soluzioni dell’equazione tg x = 1 associata alla disequazione sono: x = 45° e x = 225°

Si vede chiaramente che gli angoli la cui tangente è maggiore di 1 sono associati a quei punti che cadono o nell’arco AP, o nell’arco BP’ o nell’arco CA, esclusi oltre i punti B e C, ove non esiste la tangente, anche i punti P e P’ perché la disuguaglianza è stretta. Pertanto le soluzioni della disequazione nell’intervallo [0°; 360°] sono:

0° ≤ x < 45° V 90° < x < 225° V 270° < x ≤ 360°

Poiché per la disequazione sono richieste le soluzioni in R, consideriamo per la periodicità della funzione tangente il solo angolo che cade in [0; π ], cioè nella semicirconferenza situata nel 1° e 2° quadrante; pertanto i punti di ordinata minore di sono quelli che cadono o nell’arco AP o nell’arco BC, con esclusione del solo punto B, dato che a la tangente non è definita.

La disequazione, dunque, nell’intervallo [0; π ], è verificata per

pertanto in R le soluzioni si ottengono aggiungendo alle soluzioni precedenti i multipli di π, ovvero:

Scriviamo la disequazione in forma canonica:

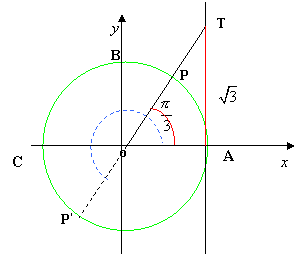
Si tratta di determinare gli angoli x la cui tangente è maggiore di . Per determinare tali soluzioni ci serviamo, come al solito, della circonferenza goniometrica. Tracciata dunque la circonferenza goniometrica e la retta tangente nel punto A, individuiamo su tale retta il punto T di ordinata e i punti P e P’ della circonferenza ad esso associati, vedi figura:

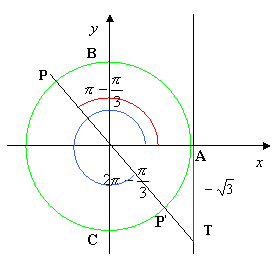
Le soluzioni dell’equazione associata alla disequazione sono:

Come si osserva dalla figura, vedi anche schema generale delle soluzioni, tutti e soli gli angoli aventi tangente maggiore di sono quelli associati ai punti della circonferenza che si trovano o nell’arco AB o nell’arco PC o nell’arco P’A, esclusi oltre i punti B e C, in cui non è definita la tangente, anche i punti P e P’, essendo stretta la disuguaglianza; pertanto le soluzioni della disequazione sono: